对于对数轴缩放,MajorUnit(在线文档 'MajorUnit属性')作为一个乘数的每个周期,提供了一个提示注释间距在每个周期内的对数的底基值。即(MajorUnit *基周期值)大约是每个周期内的注释增值。对于整数的对数基准值,结果通常是准确的。对于浮点值,注释是以很好的数字为线性缩放的。
关于UnitMajor以及Logarithmic坐标轴的详细解释
通常,当使用对数刻度时,一个图表轴的范围将跨越多个周期的对数基数。在这些情况下,对MajorUnit来说通常的线性规范不再是有道理的,作为一个适当的值的一个给定的周期为上一个或下一个周期是没有意义的。对于MajorUnit设置的值而言,它必须是相对于对数基数的周期。
如果这对你没有意义,要想一想,固定的,增量的值,你可以使用以下的轴:

根据上面的推理,在对数坐标轴的图,假设MajorUnit 指定每个周期的基础值的分数。考虑下面的例子:
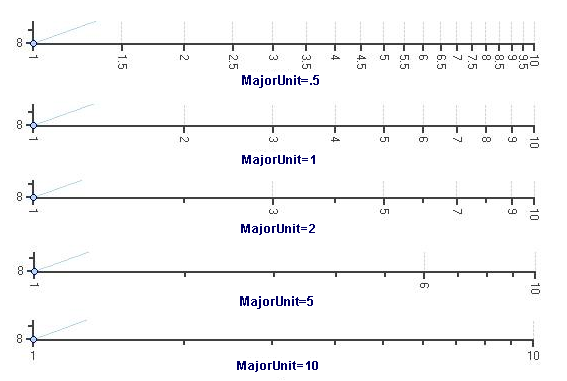
在每一种情况下,基准周期值为1。每个周期的下一个标注值=前一个数+(基数周期* MajorUnit)。MajorUnit 的最大值是LogarithmicBase。MajorUnit的自动值始终是LogBase。
当所有的注释值被计算,一个很好的四舍五入算法将应用到数值,使得该数值容易被阅读。该行为可能有点奇怪,但它是可容纳任何对数的基数,同时获取的标注的数值也是容易阅读的。
例如,以上绘图区是以10为底的常用对数,但是同样也有固有的其他底数值,比如说以2为底,以x为底等等。
查看其它